在二维平面上计算出两个由直线构成的矩形重叠后形成的总面积。
每个矩形由其左下顶点和右上顶点坐标表示,如图所示。
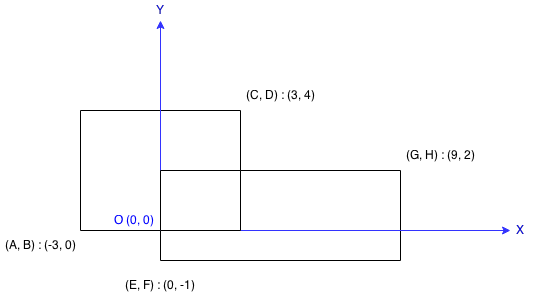
示例:
输入: -3, 0, 3, 4, 0, -1, 9, 2
输出: 45
理解题意:
- 两个矩形重叠后的总面积(笔者看成重叠部分的面积了)
- 两个矩形不一定会发生重叠,两个矩形的可能情况为:完全重叠/部分重叠/无重叠部分
思路:
计算出两个矩形总面积,减去重叠部分的面积,两个矩形的总面积很容易计算:(C-A) * (D-B) + (G-E) * (H-F) ,于是,我们的关键点就转变成了计算出重叠的部分,我们先计算两个矩形无重叠部分的情况,他们的重叠部分面积为0,假若有重叠,则计算重叠面积,利用观察法(对,你没看错)可以得出计算重叠部分的面积
判断无重叠部分:
# 当一个矩形的上边缘比另一个矩形的下边缘的还要低,或者一个矩形的最右边比一个矩形的最左边还要小则可以判断他们无重叠
C < E || G < A || B > H || F > D
计算重叠部分:
/*
当一个矩形存在重叠部分时,将4个x坐标点和4个y坐标点排序,我们会发现,第二个和第三个左边点的x坐标差、y坐标差分别构成了重叠部分矩形的宽和高,于是,重叠部分的面积计算就可以为:
*/
let xarr = [A, C, E, G].sort((a, b) => a-b)
let yarr = [B, D, F, H].sort((a, b) => a-b)
let repeat = (xarr[2] - xarr[1]) * (yarr[2] - yarr[1])
编码实现:
/**
* @param {number} A
* @param {number} B
* @param {number} C
* @param {number} D
* @param {number} E
* @param {number} F
* @param {number} G
* @param {number} H
* @return {number}
*/
var computeArea = function(A, B, C, D, E, F, G, H) {
let res = (C-A) * (D-B) + (G-E) * (H-F);
if (C < E || G < A || B > H || F > D) { // 判断是否存在重叠部分,不存在则直接返回各自相加部分
return res ;
}
let xarr = [A, C, E, G].sort((a, b) => a-b) // x坐标点排序
let yarr = [B, D, F, H].sort((a, b) => a-b) // y坐标点排序
return res - (xarr[2] - xarr[1]) * (yarr[2] - yarr[1])
};